
The GIF images were generated by linking into the Thomas? Boutell's gifdraw library by Quest Protein Database Center, Cold Spring Harbor Labs.
In the current collection, blue represents an even pair while odd pairs are yellow (or red).
This is the arrangment produced for n=31 according to the pattern in the Roy O. Davis paper:

This is the Davies pattern for 32:

This is the first langford sequence produced by the standard algorithm. The 96's are in the first position. Most of the larger numbers are all over to the left. I.e this is the first "lexicographic" solution.

Compare the above with the Davies pattern for 96:
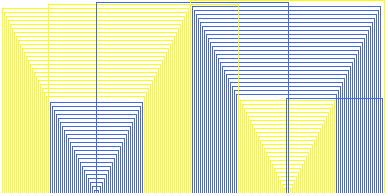
Dave Moore, Bristol England, air-mailed me langford sequences for 200 and 300 constructed by his own method. I can see how he starts out, but am not clear on how he manages to finish a particular sequence. I've converted his 200 into graphics so you can see too. Compare with the Davies pattern for 200.
Here are images for the first algorithmic solutions to various n's:
 31
31
 32
32
 35
35
 36
36
 39
39
 40
40
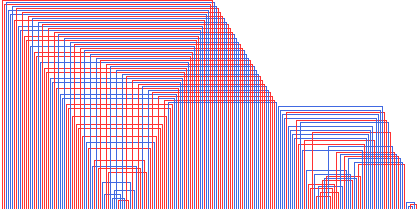 100
100
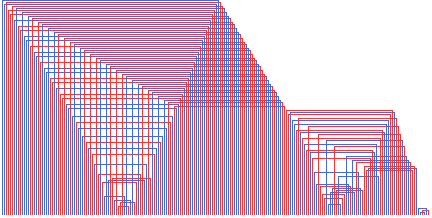 107
107
Not particularly interesting. I'm just experimenting and have these up so that I can view them myself. I really don't expect there to be information here, I was looking for a clue to why 31, 32, and 35 take so few ops to get to, but 36 and 39 take so many ops.
Back to John Miller's Langford Page
Created By: john@timehaven•us