Langford's Problem
Please cite this page if re-publishing any of my text or diagrams. See the Creative Commons License below.
Please send additions, corrections, or notifications to john @ timehaven . us.
Thanks.
Please cite this page if re-publishing any of my text or diagrams. See the Creative Commons License below.
Please send additions, corrections, or notifications to john @ timehaven . us.
Thanks.
Langford's problem is named for Scottish mathematician C. Dudley Langford who once observed his son playing with colored blocks. He noticed that the child had piled three pairs of colored blocks such that there was one block between the red pair, two blocks between the blue pair, and three blocks between the green pair as in the graphic above.
Langford added a yellow pair, and came up with a solution for four pairs:
These solutions for 3 and 4 pairs are unique. Reversing the order is not significant, because all you have to do is stand on your head, or, walk around to the other side of the arrangement and view it from that side.
Generalizing from colors to numbers, the above became 312132 and 41312432. Langford's 1958 submission to Mathematical Gazette gave one arrangement each for 7, 8, 11, 12, and 15 pairs of numbers. He noted that arrangements didn't seem possible for 5, 6, 9, or 10 pairs, so he called for a theoretical treatment — What values of 'n' were solvable?
The proof of why 5, 6, 9, 10, etc are impossible is fairly simple, and can be found in the Roy O. Davies paper, ON LANGFORD's PROBLEM II in Mathematics Gazette, 1959, v43.
In general, Davies proved that 'n' must be a multiple of four, or one less. In the remarks at the end of his paper, Davies wondered how many solutions there were for different n's, and stated (wrongly!) that for n=7, there were 25 solutions.
Details. Consider in general the pair of k's in the arrangement, where k is any number from 1 to n. If the first k is in position p, then the other k must be in position p + k + 1. For example, the one's might be in position 8 and 10 in an arrangement, with position 9 separating them.
Let's say that all the various values for p (the position of the first number for a given pair) are stored in an array 'P', so that P1 holds the position of the leading (leftmost) 1, and P2 holds the position of the leading 2. The positions of the leading numbers of each pair are kept in P1 through Pn.
We can form the summation of numbers (Pk) and (Pk+k+1) for k=1,2,...n. But the positions of all the individual numbers must be the same numbers (1, 2, ... 2n) in some order. Therefore summation for k=1,n of (2Pk+k+1) can be equated with the summation of 1, 2, ... 2n, which is n(2n+1).
Rearrange terms to solve for the summation of just the Pk's, which has to be an integer. That's the key! That is, whatever the summation might be for a given solution, it is a whole number. The final step is left for the reader, which shows that n must be of the form 4m or 4m-1 in order for things to be integral.
See 'Odd/Even Parity as key to Solvability' below for a simpler explanation.
Martin Gardner posed n=4 in a collection of short problems in Mathematical Games, November 1967, Scientific American. He told readers that month that no solutions were possible with 5 or 6 pairs, but that there were 25 unique arrangements for n=7, without citing a reference. (There later turned out to be 26 solutions for n=7.)
In December 1967, Gardner explained that Langford's Problem has been shown to be solvable when n is any multiple of four or one less. Martin said no one knew how to determine the number of distinct solutions for a given number of pairs except by exhaustive trial and error.
The gauntlet was down, and the stage was set for a popular computing problem.
It should be noted that at around the same time, the problem also appeared in Design Electronics and the Daily Telegraph, both British publications. So people in England and elsewhere found themselves working on Langford's Problem.
Early in 1968, as a college freshman,
I (John Miller) programmed Langford's Problem and found 26 (not 25!) solutions for n=7 and 150 solutions for n=8.
Four others did likewise with computers. Two others solved n=7 by hand
.
In addition, E.J.Groth cracked n=11 (17,792 solutions) and n=12 (108,144).
Martin Gardner published these results in his March 1968 column.
Since 1968, the number of solutions for 15, 16, 19, and 20 have been calculated by multiple people using various techniques. 23, 24, and 27 were computed by one team. 27 and 28 were computed by yet another team.
Planar solutions (below) are less intensive due to pruning (?). P31 and P32 were determined in 2018.
I've been informed of a paper by Dr Zan Pan that gives an asymptotic formula estimating the number of Langford and the Skolem sequences! The paper goes over the formula, and demonstrates its performance with a table of estimated vs actual values and the percentage difference. More comments ASAP (Fall 2022?), with a page dedicated to Dr Pan's work.
Does this work reflect the intrinsic nature of Langford's problem? Other results on this Langford page are either enumeration or calculation by algebraic methods. (Of course God's Formula
would be some kind of integer-based combinatoric formula.)
Here is a direct link to the current version of Zan Pan's paper, Conjectures on the number of Langford sequences, which contains his contact information. Link updated 4/17/22 [PDF]
We use the notation L(2,n) to indicate the number of unique solutions for Langford's Problem with n pairs of blocks. There are several variations of Langford's Problem. We refer to the number of solutions to those variants with letters L, V, P, Q as below.
See Variations, Planar Solutions, and End-Run Planar solutions below.
We use the notation L(s,n) or V(s,n) to indicate the number of solutions for (L)angford's Problem or the Nickerson (V)ariant where:
Example: L(4,24) = 3, denotes that there are three solutions with quadruplets for n=24.
We also sometimes use the same notation to refer to the set of all solutions, whether known or unknown. So in a scalar context, L(s,n) is an integer. In another context it could refer to the particular problem in general (for now, anyway).
Let's also use P(2,n) to refer to the number of planar solutions for n pairs. Eg: P(2,8) = 4.
Molinari proposes to use Q(2,n) to refer to the number of end-run planar solutions for n pairs. Eg: Q(2,8) = 24. The Q sequence has not been added to the Table of Solutions yet. JM 3/2018.
Here is a timeline (2002-2022) of work done on Langford's by Mike Godfrey, Ron van Bruchem, Michaël Krajecki, Christophe Jaillet, Alain Bui, Team Assarpour-Liu, Boris Dimitrov, Rory Molinari, Zan Pan, and John Miller.
For a complete annotated timeline, please go to the [TIMELINE page].
A variant of Langford's Problem has the second number of each k-pair occur in the kth place after the first, so that there are k-1 other numbers between the two k's. The singular variant solution for n=4 is 42324311. R. Nickerson proved this is possible whenever n is of the form 4m or 4m+1. See Bibliography.
Note the 1's are always together in the variant. [So the variant is like adding a pair of 0's to the classic problem - no blocks between the two zeroes. Skolem variant?]
Arrangements can be made using triplets as well, where the outer elements of each triplet are separated from the middle element in the triplet, as in this arrangement. There are 9 other numbers between the 9's here:
Nine triplets [1-9] can be arranged in 3 ways. See the table below for other results.
Such triplet sequences can be done for any n≥9 that is of the form 9k-1, 9k, 9k+1. Mathematically, we write this as n ≡ (-1,0,1) mod 9, pronounced n is
congruent to -1, 0, or 1 modulo 9
. [Also could write n ≡ (0,1,8) mod 9.]
Details. Frank Ruskey found at least one solution with triplets for n = 26,27,28, 35,36,37, 44,45,46, 53,54,55, 62,63,64 (solutions for 26,27,28 were also found by Brad Jackson at San Jose State). The existence of these sequences is proven in the Levine paper.
The triplet arrangement can also be done with the Nickerson variation. I suspect that the criteria for solvability of the variant with triplets is n ≡ (0,1,2) mod 9. [Isn't this in the paper??]
By a theorem of Levine, there are no perfect 4-sequences unless n ≡ -1, 0 (mod 8). (Theorem 2 in The Existence of Perfect 3-Sequences. Really? I don't see that literally stated there. I don't know where I got the congruence from. --jem2020)
Extensive search of higher orders reportedly discovered solutions with quadruplets for n = 17, 18, 19, 20, and later, results for n=24. (These results by Saito & Hayaska seem to be defective! They built a special purpose circuit to perform their searches. Study to be continued...)
Saito & Hayaska claim no known quintuplets for n≤24, and no sextuplets for n≤21.
A subset of the solutions are planar
if lines connecting all pairs can be drawn without crossing, as in the following example for n=8 provided by D. E. Knuth:
The connection must be simple and direct, not doing an end run around from top to bottom.
This is sequence number A125762 on OEIS.org, included in the Table of Solutions below. Knuth calculated up to n=28.
Knuth's values have all been independently confirmed by a second program by Boris Dimitrov, who is currently (2017) working on extending these results. We have a page for Boris's work: [HERE].
Rory Molinari also confirmed Knuth's results, and extended the known solutions to P(2,32).
Exercise. Adapt the classic search algorithm or invent your own Algorithm X to generate only planar solutions for a given n.
Rory Molinari has explored a variation of planarity, where connecting lines are allowed go around the end of the arrangement in order to avoid crossing. See the END RUN section on his page [LINK].
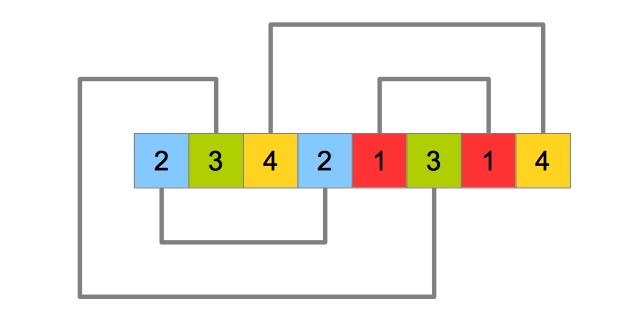
A variation from Colombia — having to do with a 'Sentinel Pair' that allows only one number from each pair between them! We call it The Colombian Variant.
10 students sit in a circle. Is it possible for one student to move 1 place clockwise, one student 2 places clockwise, one student 3 places clockwise, and so on, all the way up to tenth student moving 10 places clockwise (back to his/her own seat) and ALSO end up one student per seat? — Tweeted @jamestanton on Dec 30 2018.
Discussion followed! Are Tanton's Chairs like Langford Pairs? See my investigation of Tanton's Chairs.
Sections having to do with Enumeration...
TABLE of Solutions for classic problems and known variants. [TABLE]
List of Contributors (for Google): Andrew Burke, Assarpour-Liu Team, Bernardo Recamán Santos, Boris Dimitrov, C. Dudley Langford, Dave Moore, Donald Knuth, E. J. Groth, Frank Ruskey, Freddy Barrera, Frederick Groth, Glen F. Stahly, John Boyer, John Miller, Krajëcki Teams, Malcolm Holtje, Mike Godfrey, Richard Noble, Robert Smith, Ron van Bruchem, Rory Molinari, Roy O. Davies, Saito & Hayaska, Thomas Starbird.
Detailed TABLE of Contributors and their Contributions: [TABLE]
Let's say that you wanted to see one solution for n=100, just for your own satisfaction.
In one paper, Roy O. Davies gives a pattern for constructing a single solution for any valid n. Using this pattern, a computer program can instantly generate a solution for n=40,000 or other large number. See the Graphics section below for some examples. A Perl program is included for your examination / reference.
Dave Moore submits an approach based on what he has observed, for your edification. You can see a graphical representation of his method on the Graphical Representations page below. [should just add the graphics to dave-moore-html!]
Stephen Scattergood has contributed to Dave Moore's method (in an effort to complete it), and analyzed planar solutions. [Should try to better summarize Steve's work here!]
Scattergood says: One learns a lot by going after this problem... Not necessarily solving much about the problem, but a lot about whatever methods you tried to use.
An arrangement of pairs of numbers 1,1, 2,2, 3,3, ... n,n will have 2n positions numbered 1..2n. Half the positions will be oddly-numbered, the other half evenly-numbered.
An even pair will take an odd position and an even position, no matter where the pair is in the arrangement. For example, if Left 2 is in position 1, the Right 2 must be in position 4. That's encouragingly balanced parity!
However, an odd pair will take either two odd positions or two even positions. Therefore the odd pairs must occur in pairs themselves to preserve parity
if there is any hope of covering all the positions in a full arrangement. So, there must be an even number of odd pairs. This happens only when n is 3, 4, 7, 8, 11, 12, 15, 16, ..., 4m-1, 4m.
Exercise. Does this mean that half of the odd pairs must be in even positions, and half are in odd positions? What does this mean for the even pairs?
Shows a hypothetical Langford Machine
finding one solution for n=7 (seven pairs of colored blocks).
Click on the image to activate the YouTube video. The machine stops after finding the first solution. Machine states are:
1 Initialization F Test Fit of pair S Shift O Test Overflow (reached end of shift register) I Insert Pair R Remove Pair (back to shift reg) P Pop Pair off stack into shift register at position 1 U Push Pair back onto pair stack Z Propundity (Terminate)
Successive solutions can be found by removing the lower pairs and continuing the search. See the section 'An Array-Based Non-Recursive Algorithm', in my Algorithmic Notes below.
On the this page, details are given about the systematic enumeration of Langford sequences. [Algorithmic Solution Notes]
On this page, you'll find graphics representing various aspects of Langford sequences. [Graphical Representations] For example, the following graphic shows the state of 19 as it was on Jan 30, 1997. Blue represents even numbers, yellow, odd.
Here's a fun graph of the path through 8 pairs of blocks [5286235743681417]. Don't traverse the black lines — follow the red arrows. Notice the cycle of 4 blocks between the two 4's, and so on. It's like taking a tour of a city, without walking over any of the bridges!
The above graph was part of my talk at G4G11. (See My G4G11 Talk and Papers, below.)
A Langford graph has 2n nodes and 3n-1 edges. The graph will have 2 nodes of degree 2, and 2n-2 nodes of degree 3. This is because the two end blocks have either a left or right connection (not both), plus each end block has has one edge for their twin, making two edges. Interior blocks all have a left, right, and pairing edge, for three edges.
Click below to play with a force-directed graph of a Q-Planar solution of Q(2,12).
A solution for L(2,11) is shown above. Can you tell which dots represent the two end blocks?
This concerns the number of algorithmic operations required to get to the first solution of L(n,2). N=39 and n=47 take billions of operations, while other n's take only hundreds or less. To make things more bizarre, adjacent n's sometimes take the exact number of operations to reach their first solution even though it couldn't be the same search tree. (Or could it?). [A Very Odd Observation]
For my senior thesis at WSU (1972), I designed (but did not build) a sequential logic circuit for the search algorithm.
Saito & Hayasaka at Miyagi Tech College in Japan designed and built special purpose computers to check for the existence of solutions for various higher order tuples. Their results are questionable! See reference in bibliography.
In the 1960s, E. J. Groth used Langford pairings to construct circuits for integer multiplication. Need reference! Knuth mentions in his Volume 4a.
Charles Dudley Langford was born in Highgate (near London) in October 16, 1905. He contracted polio at age 12.
Langford started out as an industrial chemist and was a member of Royal Chemical Society. He became a passionate Maths teacher who thought about all kinds of mathy problems, publishing 30 notes in Mathematical Gazette. He co-authored a paper on Hinged Dissections with Martyn Cundy, and corresponded with Harry Lindgren. At some point, he moved to Ayrshire, Scotland.
Little did we know that Langford was dying during the time we were cranking away on his problem using computers in 1967 and 1968. He died January 11, 1969 at age 63, in Girvan. His son, Charles Andrew Langford was born in 1938 in Girvan. Langford is buried in Girvan, Ayrshire district of Scotland, in the East Doune (Girvan) Cemetery.
It is unknown if Langford himself somehow made money with a puzzle based on LP.
The Bibliography is on a separate page. Click to visit that page.
The proofs of possibility take advantage of the summations formed by the positions of pairs and their requisite separation in an arrangement. For it to all hold true (integral) n must be of the form 4m or 4m-1.
The Roy Davies paper (and others) gives patterns for constructing a single langford sequence (arrangement) for any given n, as a demonstration (construction) proof for a theorem that the solutions are not only possible but at least one exists for each feasible value of n.
Martin Gardner revisits Langford's Problem in Mathematical Magic Show, published by Alfred A. Knopf, ISBN 0-88385-449-X, first and second editions.
Volume 1 of The Art of Computer Programming [TAOCP] came out in 1968. Volume 4a (Chapter 7) of TAOCP, Combinatorial Searching, uses Langford's Problem to illustrate!
Here is a video of my 12 minute G4G11 talk on Langford's Problem:
Here's a PDF of paper that I presented at G4G11, Langford's Problem, Remixed: [PDF].
Here is the YouTube video of my 7 minute G4G14 talk, which was posted Sept 6, 2022. Be sure to catch the special announcement at the end.
More Fun with Langford's Problem - G4G14 Apr 2022
Here is my More Fun...
paper, which was presumably included in the G4G14 Gift Book or packet, anyway
[274K PDF].
Except where otherwise noted, content on this site is licensed under a Creative Commons Attribution 4.0 International license [CC BY 4.0]. All I ask is notification and attribution. Please send notifications to john @ timehaven . us. Thanks!
John E. Miller, Portland, Oregon.